Напряженность электрического поля задается формулой. Напряженность электрического поля. Принцип суперпозиции полей — Гипермаркет знаний
Лекція 19.
1. Электростатическое поле в вакууме
1.1 Дискретность электрического заряда. Закон сохранения электрического заряда
Источником электромагнитного поля служит электрический заряд – внутренняя характеристика элементарной частицы, определяющая ее способность вступать в электромагнитные взаимодействия. Различают два вида электрических зарядов – положительный и отрицательный. Электрический заряд дискретен – заряд любого тела составляет целое кратное от элементарного электрического заряда e =1,610 -19 Кл. По знаку заряда все элементарные частицы можно разделить на два класса: отрицательно заряженные (например, электрон) и положительно заряженные (протон, позитрон и др.). Один из фундаментальных строгих законов природы – закон сохранения электрического заряда: алгебраическая сумма электрических зарядов любой замкнутой (электрически изолированной) системы остается постоянной, какие бы процессы ни происходили внутри этой системы.^
1.2 Закон Кулона. Напряженность электрического поля
Взаимодействие между неподвижными электрическими зарядами осуществляется посредством электрического поля. Представление об электрическом поле было введено в 30-х годах XIX в. английским физиком М. Фарадеем. Согласно Фарадею каждый покоящийся заряд создает вокруг себя электрическое поле; поле одного заряда действует на другой заряд, и наоборот, – так осуществляется взаимодействие между зарядами.
Сила взаимодействия между двумя точечными неподвижными зарядами определяется законом Кулона: два точечных неподвижных заряда взаимодействуют друг с другом с силой, пропорциональной произведению зарядов и обратно пропорциональной квадрату расстояния между ними:
| , | (1.1) |
где k - постоянная, зависящая от выбора системы единиц. Сила Кулона направлена по линии, соединяющей заряды. По третьему закону Ньютона кулоновские силы приложены к разным зарядам и направлены либо навстречу друг другу (если заряды разноименные), либо в противоположные стороны (если заряды одинакового знака). В СИ постоянная
 , где
0
- электрическая постоянная СИ,
0
=
8,85
10
-12
Кл
2
/(Н
м
2
).
, где
0
- электрическая постоянная СИ,
0
=
8,85
10
-12
Кл
2
/(Н
м
2
).
Таким образом, для зарядов, расположенных в вакууме, закон Кулона имеет вид
 . .
| (1.2) |
Электрический заряд в СИ измеряется в кулонах. Один кулон - это такой заряд, который протекает через поперечное сечение проводника за 1с при неизменной силе тока, равной 1А.
Силовой характеристикой электрического поля является напряженность
 – векторная величина, модуль которой равен силе, действующей со стороны электростатического поля на единичный заряд; а направление совпадает с направлением силы, действующей на положительный заряд
– векторная величина, модуль которой равен силе, действующей со стороны электростатического поля на единичный заряд; а направление совпадает с направлением силы, действующей на положительный заряд
гдеЕ
с
– напряженность электростатического поля в среде.
Если электростатическое поле создается несколькими зарядами, то в соответствии с принципом суперпозиции суммарная напряженность поля в некоторой точке определяется как векторная сумма напряженностей, создаваемых в этой точке отдельными зарядами:
  | (1.5) |
1.3. Расчёт напряжённости поля точечного заряда и электрического диполя
1.3.1. Напряженность поля точечного заряда

Рис. 1.1
^
1.3.2. Напряженность поля электрического диполя
Электрическим диполем называется совокупность двух точечных, одинаковых по величине, но противоположных по знаку зарядов, жестко закрепленных на расстоянии l друг от друга (рис. 1.2). Расстояние l называется плечом диполя, а вектор
 | (1.8) |

Рис. 1.2
дипольным моментом (электрическим моментом диполя). Дипольный момент направлен вдоль оси диполя в сторону положительного заряда (рис. 1.2).Найдем теперь напряженность поля диполя, ограничиваясь случаем r>>l
.
^
А. Напряженность поля в точке, находящейся на продолжении оси диполя
В соответствии с принципом суперпозиции напряженность поля в точкеА
(рис. 1.3)

Рис. 1.3

где  и
и
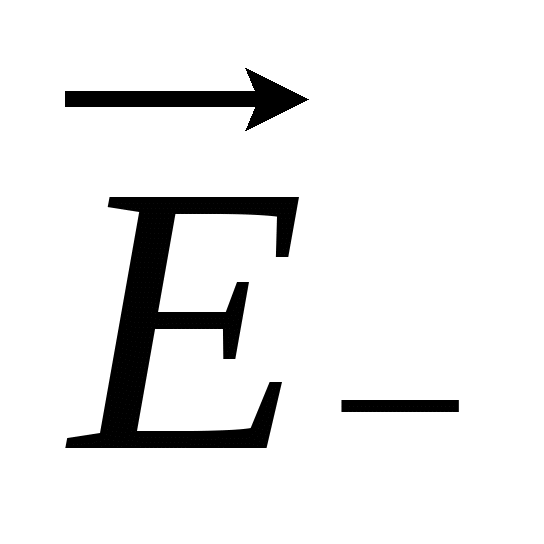 – напряженность поля, создаваемого соответственно зарядами+Q
и -Q
.
Поскольку векторы
и
направлены в противоположные стороны, то модуль вектора
будет
– напряженность поля, создаваемого соответственно зарядами+Q
и -Q
.
Поскольку векторы
и
направлены в противоположные стороны, то модуль вектора
будет ,
где в соответствии с (1.6)
,
где в соответствии с (1.6)  .
Таким образом,
.
Таким образом, 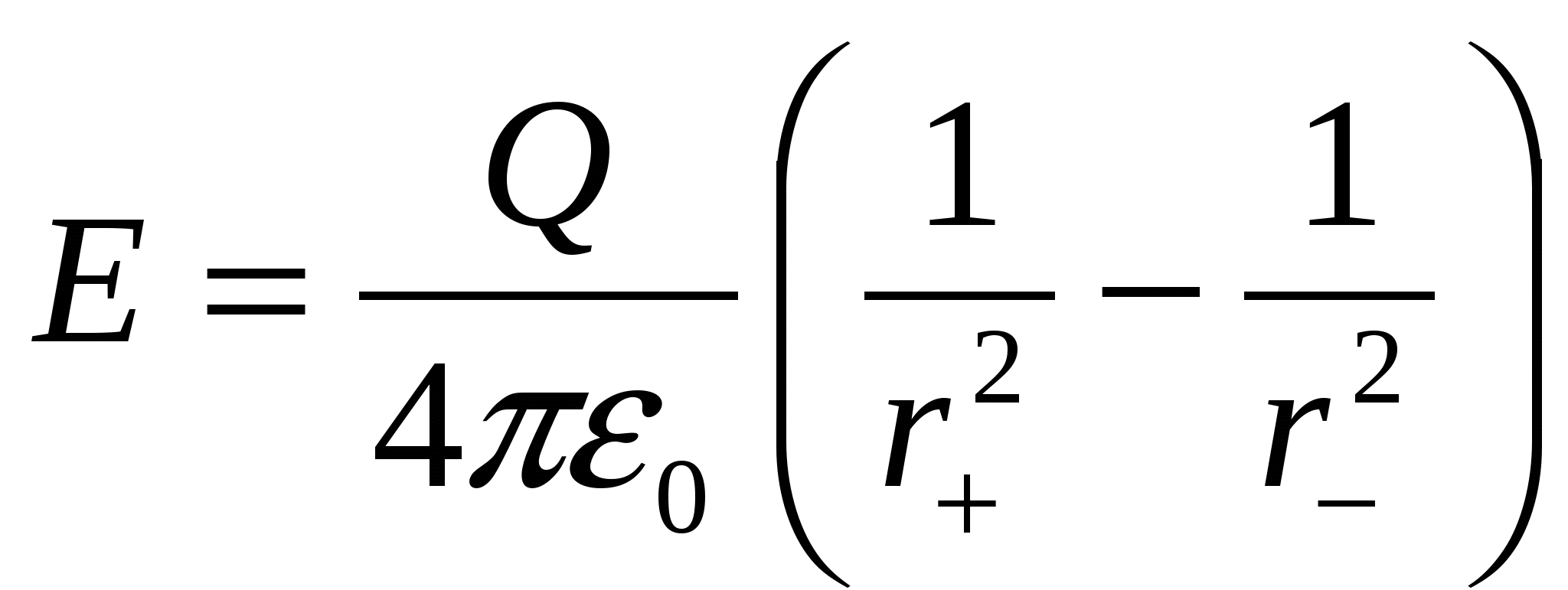 .
.
Выражение в скобках преобразуем следующим образом. Из рис. 1.3 видно, что  ,
где r
– расстояние между точкой А
и центром диполя. Далее имеем
,
где r
– расстояние между точкой А
и центром диполя. Далее имеем
 .
.
Поскольку r>>l
,
то значением  в знаменателе можно пренебречь, поэтому
в знаменателе можно пренебречь, поэтому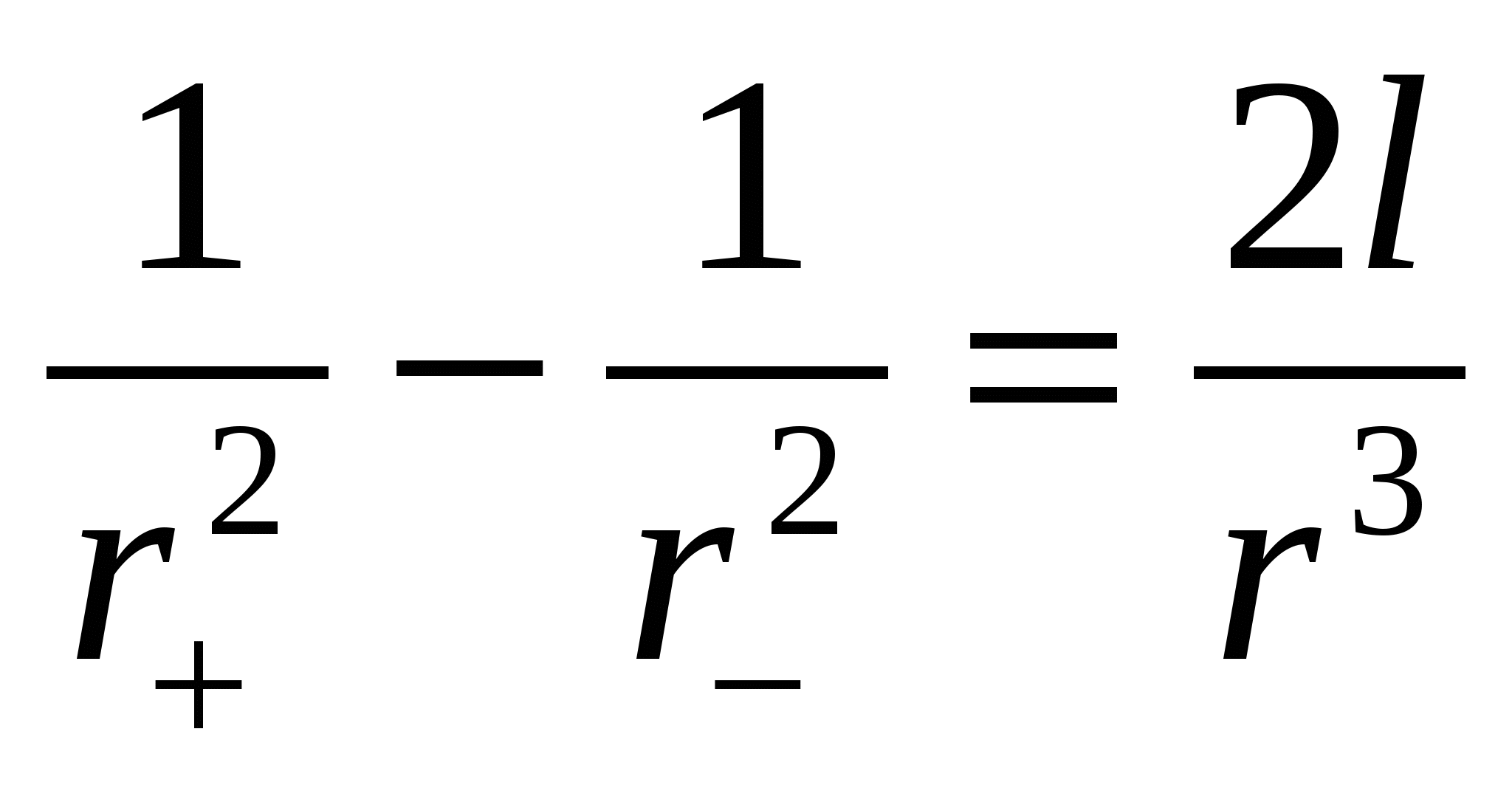 ;
;
 .
Так как Ql
есть дипольный момент, то
.
Так как Ql
есть дипольный момент, то 
Б. Напряженность поля на перпендикуляре оси диполя

Рис. 1.4
Из рис. 1.4 видно, что .Далее
.Далее ,
, ,
,
Следовательно, 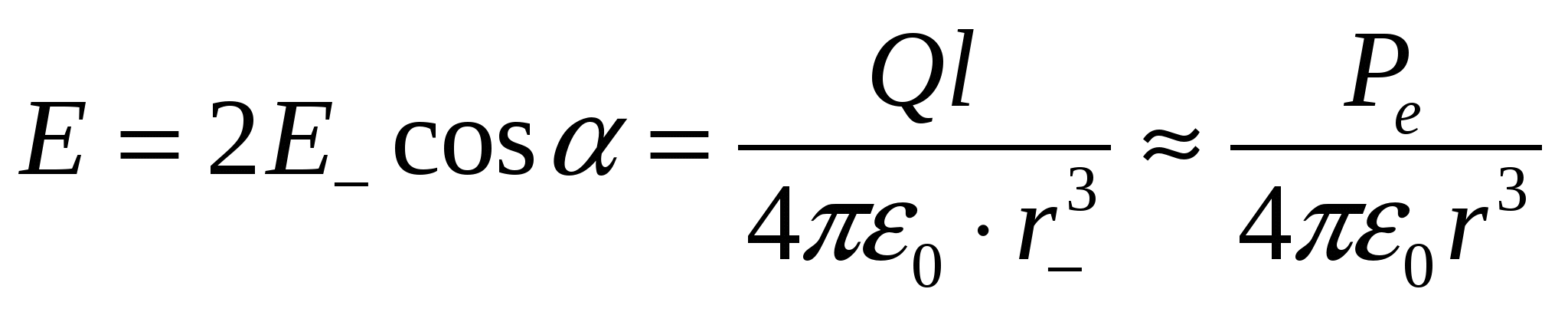 , где P
l
=Ql
– дипольный момент. Таким образом,
, где P
l
=Ql
– дипольный момент. Таким образом,
 . .
| (1.10) |
Из сопоставления (1.9) и (1.10) видно, что напряженность поля на оси диполя в 2 раза больше, чем на перпендикуляре к его оси. Отметим также, что напряженность поля диполя убывает как 1/r ‑3 , т.е. быстрее, чем для точечного заряда, где E 1/r ‑2 .
^
1.4. Силовые линии. Поток вектора напряженности. Теорема Остроградского-Гаусса
Силовой линией электростатического поля называется линия, касательная к которой в каждой точке совпадает с направлением вектора
 (рис. 1.5).
(рис. 1.5). 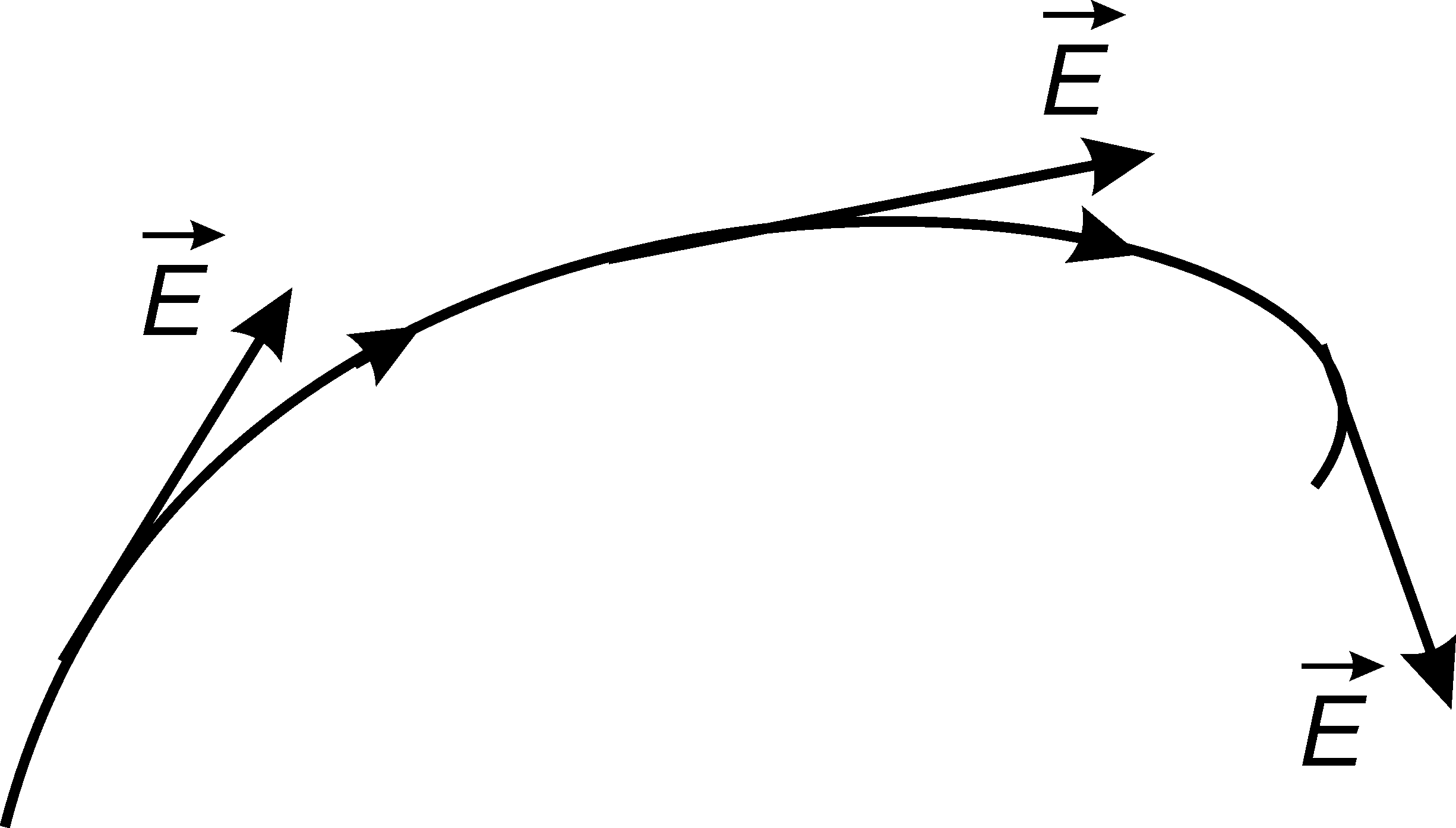
Рис. 1.5
Свойства силовых линий:
а) силовые линии электростатического поля не пересекаются;
б) силовые линии электростатического поля разомкнуты - они начинаются на положительных зарядах и заканчиваются на отрицательных (или уходят в бесконечность).
Введем понятие потока вектора напряженности поля
. По определению элементарный поток вектора напряженности через площадку dS
где  – единичный вектор, совпадающий с нормалью.
– единичный вектор, совпадающий с нормалью.
Суммарный поток вектора напряженности через какую-либо поверхность можно найти интегрированием (11.12) для всей поверхности 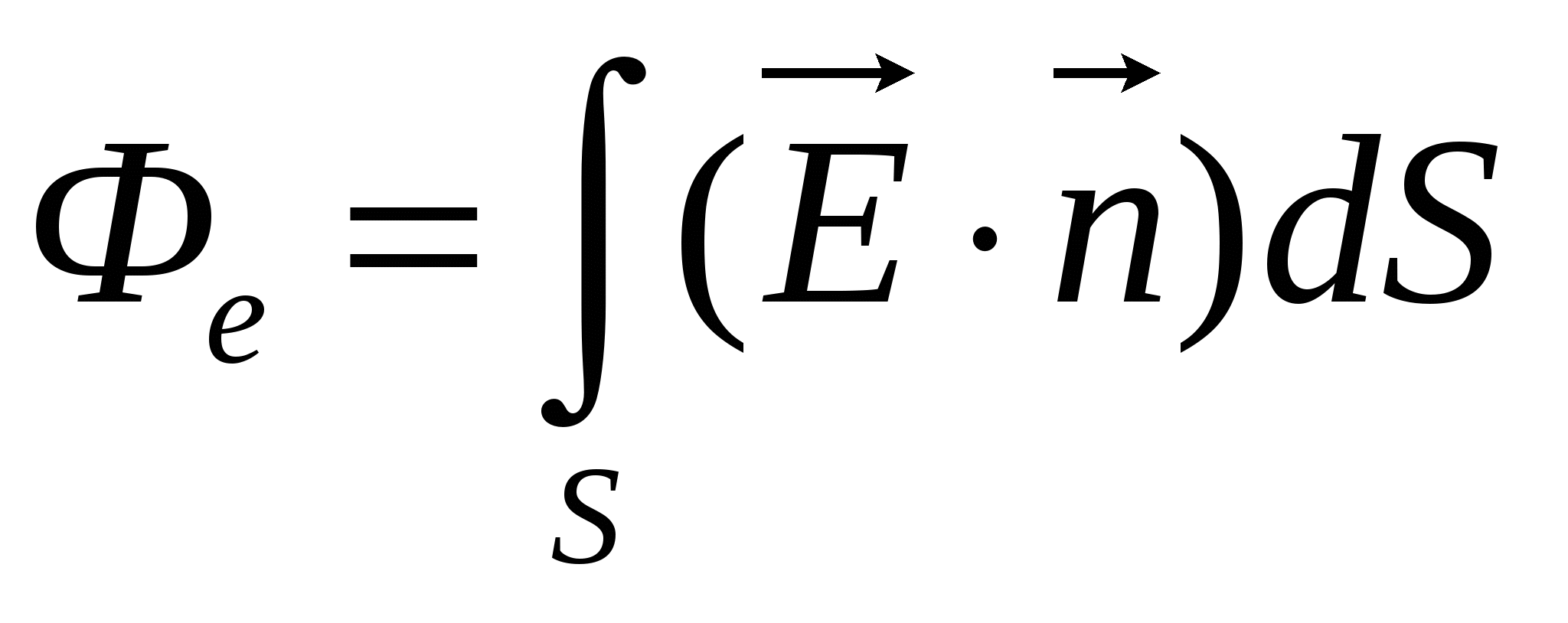 для замкнутой поверхности
для замкнутой поверхности 
Важнейшую роль в электростатике играет теорема Остроградского ‑ Гаусса, которая формулируется следующим образом: поток вектора напряженности через любую замкнутую поверхность пропорционален алгебраической сумме зарядов, находящихся внутри этой поверхности:
 , (1.13)
, (1.13)

Рис. 1.6
Доказательство . Рассмотрим простейший случай, когда замкнутая поверхность представляет собой сферу, в центре которой находится точечный заряд +Q (рис. 1.7). Выделим на сфере элементарную площадку dS . Нормаль к этой площадке и вектор совпадают по направлению, поэтому .
![]()
Рис. 1.7
Преобразуем подынтегральное выражение в (1.13) следующим образом:
Принимая во внимание, что всюду на поверхности сферы E = const , и учитывая выражение (11.6), получим:
Теорема доказана для частного случая, когда внутри сферической поверхности имеется один заряд. Доказательство легко обобщается на случай произвольного числа зарядов и произвольной замкнутой поверхности.
В суммарном потоке, который создают заряды, расположенные за пределами замкнутой поверхности, можно выделить положительную и отрицательную части, которые взаимно компенсируются. Поэтому внешние по отношению к данной замкнутой поверхности заряды в теореме Остроградского – Гаусса не учитываются.
Теорема Остроградского-Гаусса связывает заряды с создаваемыми ими электрическими полями и отражает тот факт, что источником электростатического поля служат неподвижные электрические заряды.
Эта теорема тесно связана с законом Кулона: если справедлив закон Кулона, то справедлива и теорема Остроградского-Гаусса, и наоборот. Если бы в законе Кулона показатель степени хотя бы незначительно отличался от двух, т.е. F
1/r
2+
α
, где α
–
сколь угодно малое число, то теорема Остроградского-Гаусса нарушалась бы. Справедливость теоремы Остроградского-Гаусса проверена на опыте с гораздо большей точностью, чем закон Кулона.
^
1.5. Применение теоремы Остроградского-Гаусса для расчета полей
Теорема Остроградского-Гаусса в ряде случаев позволяет сравнительно просто рассчитать напряженность электростатического поля при заданном распределении зарядов. Рассмотрим несколько примеров.
^
1.5.1. Поле бесконечной равномерно заряженной плоскости
Пусть имеется бесконечная равномерно заряженная плоскость с поверхностной плотностью заряда
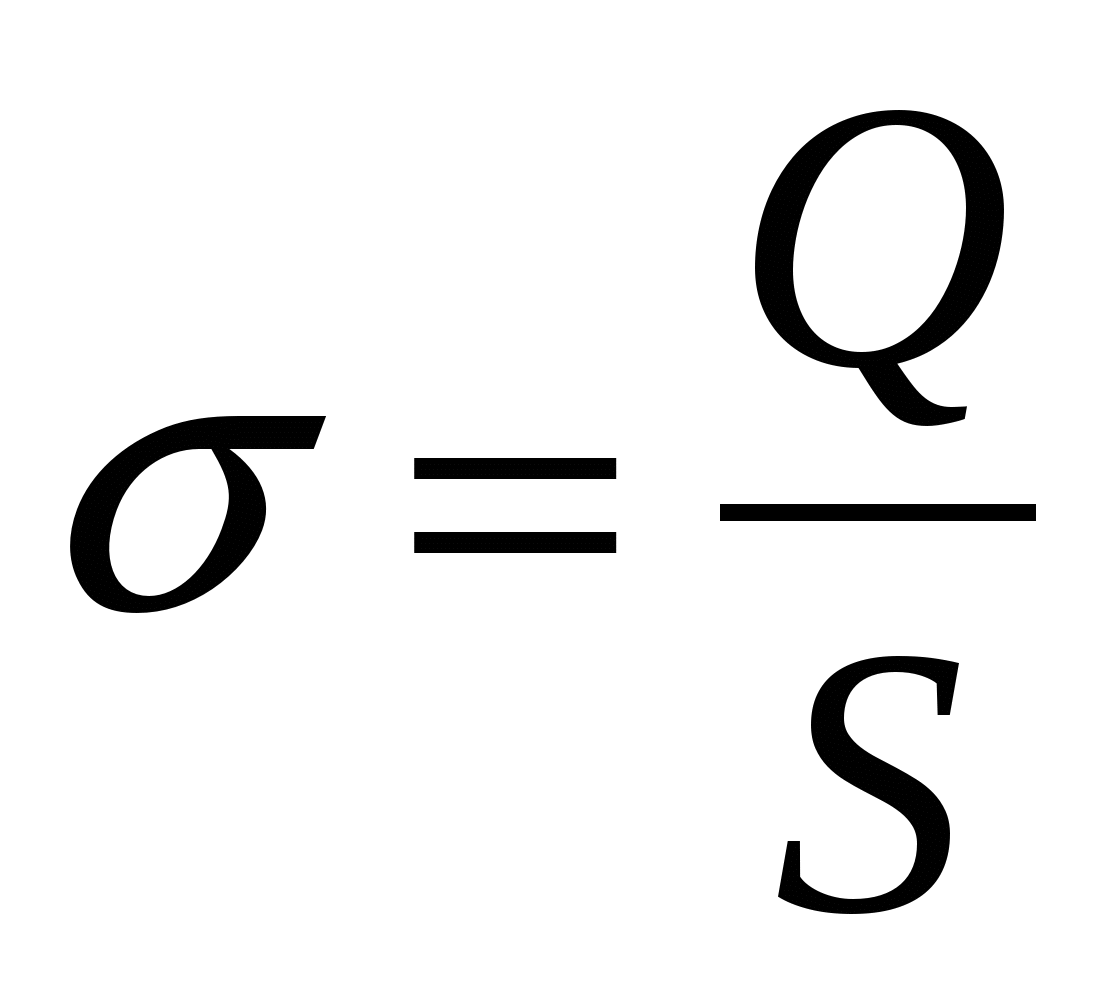 [Кл/м
2
]
[Кл/м
2
]
Из соображений симметрии следует, что вектор
должен быть перпендикулярным к плоскости. Выберем замкнутую поверхность в виде цилиндра, боковая поверхность которого ориентирована вдоль вектора
(рис. 11.8). Суммарный поток вектора
, очевидно, составляет

Рис. 1.8
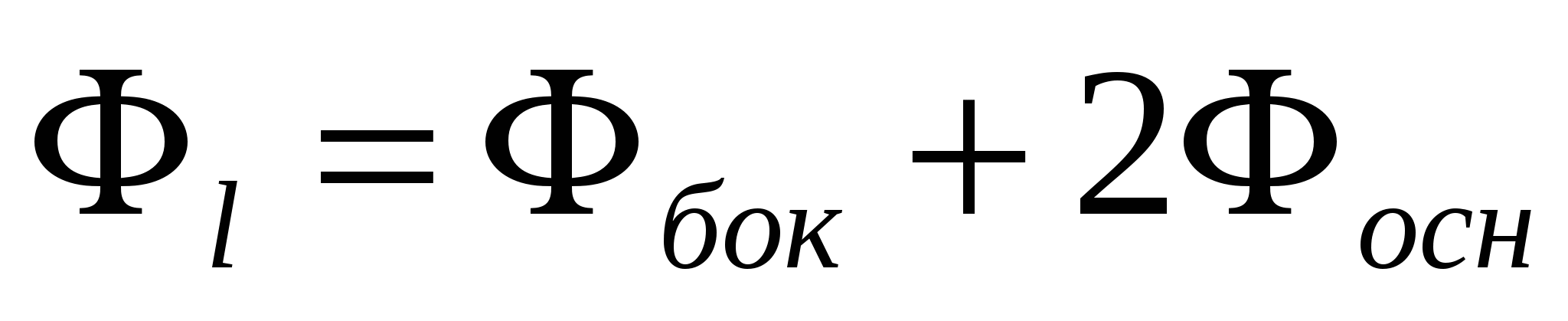 .
.
Поток через боковую поверхность равен нулю, так как (рис. 1.8):
Поток через основание цилиндра:
 .
.
Таким образом, полный поток вектора Е
через замкнутую поверхность  .
.
По теореме Остроградского-Гаусса  . Отсюда напряженность поля
. Отсюда напряженность поля
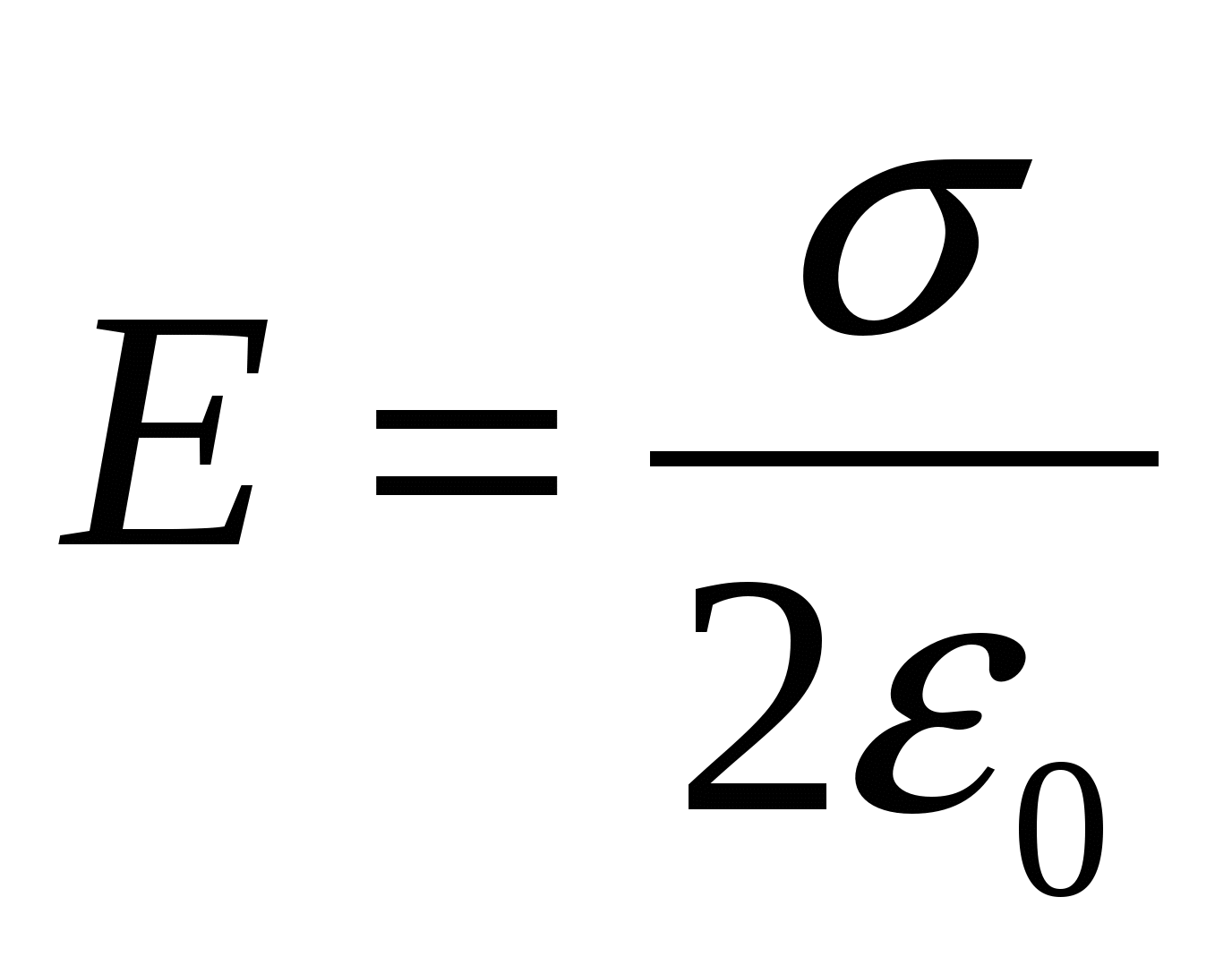 , (1.14)
, (1.14)
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, не зависит от расстояния до нее. Поле, в котором вектор напряженности одинаков по величине и направлению, называется однородным.
^
11.5.2. Поле двух бесконечных равномерно заряженных плоскостей
Рассчитаем напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, равномерно заряженными с поверхностной плотностью заряда +σ и -σ (рис. 11.9).

Рис. 1.9
Согласно принципу суперпозиции суммарная напряженность поля
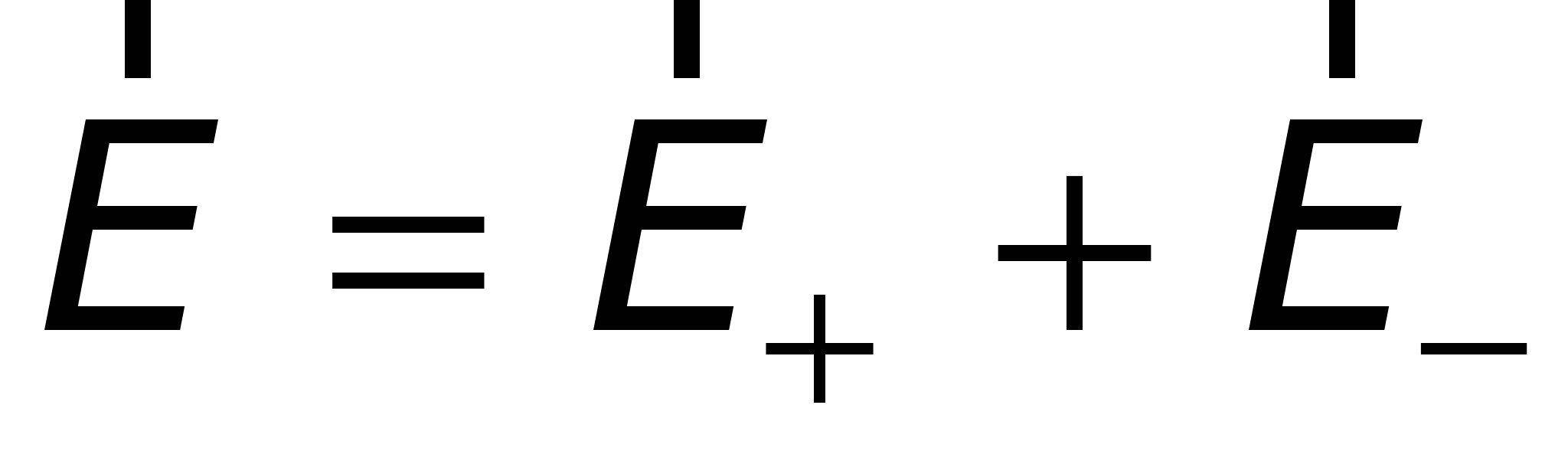 ,
,
где  и
и
 – напряженность поля, создаваемого соответственно положительно и отрицательно заряженными плоскостями.
– напряженность поля, создаваемого соответственно положительно и отрицательно заряженными плоскостями.
В областях пространства I и III (рис. 1.9) векторы и
направлены в противоположные стороны, поэтому суммарная напряженность 
В области II и
параллельны и равны по модулю, поэтому .
Используя предыдущий результат, получим
.
Используя предыдущий результат, получим  .
.
Аналогично можно показать, что если плоскости заряжены одноименно, то во внешних областях I и III напряженность поля определяется формулой (11.I5), а во внутренней области I , что используется для электростатической защиты приборов.
11.5.3. Напряженность поля бесконечной равномерно заряженной нити с линейной плотностью заряда
 [
Кл/м]
[
Кл/м]

Рис. 1.10
 . . | (1.16) |
При выводе формулы (1.16) следует выбрать замкнутую поверхность в виде цилиндра (рис. 1.10) и учесть, что вектор
 перпендикулярен к нити и поэтому поток вектора через основания цилиндра равен нулю.
перпендикулярен к нити и поэтому поток вектора через основания цилиндра равен нулю.11.6. Работа по перемещению заряда в электростатическом поле. Теорема о циркуляции вектора
Найдем элементарную работу по перемещению заряда q в поле, создаваемом зарядом Q :где – угол между силой  и направлением перемещения
и направлением перемещения  .
.
Из рис. 1.11 видно, что  .поэтому
.поэтому 
Суммарную работу но перемещению заряда q
из точки А
в точку B
получим интегрированием выражения (11.17). Используя закон Кулона, получаем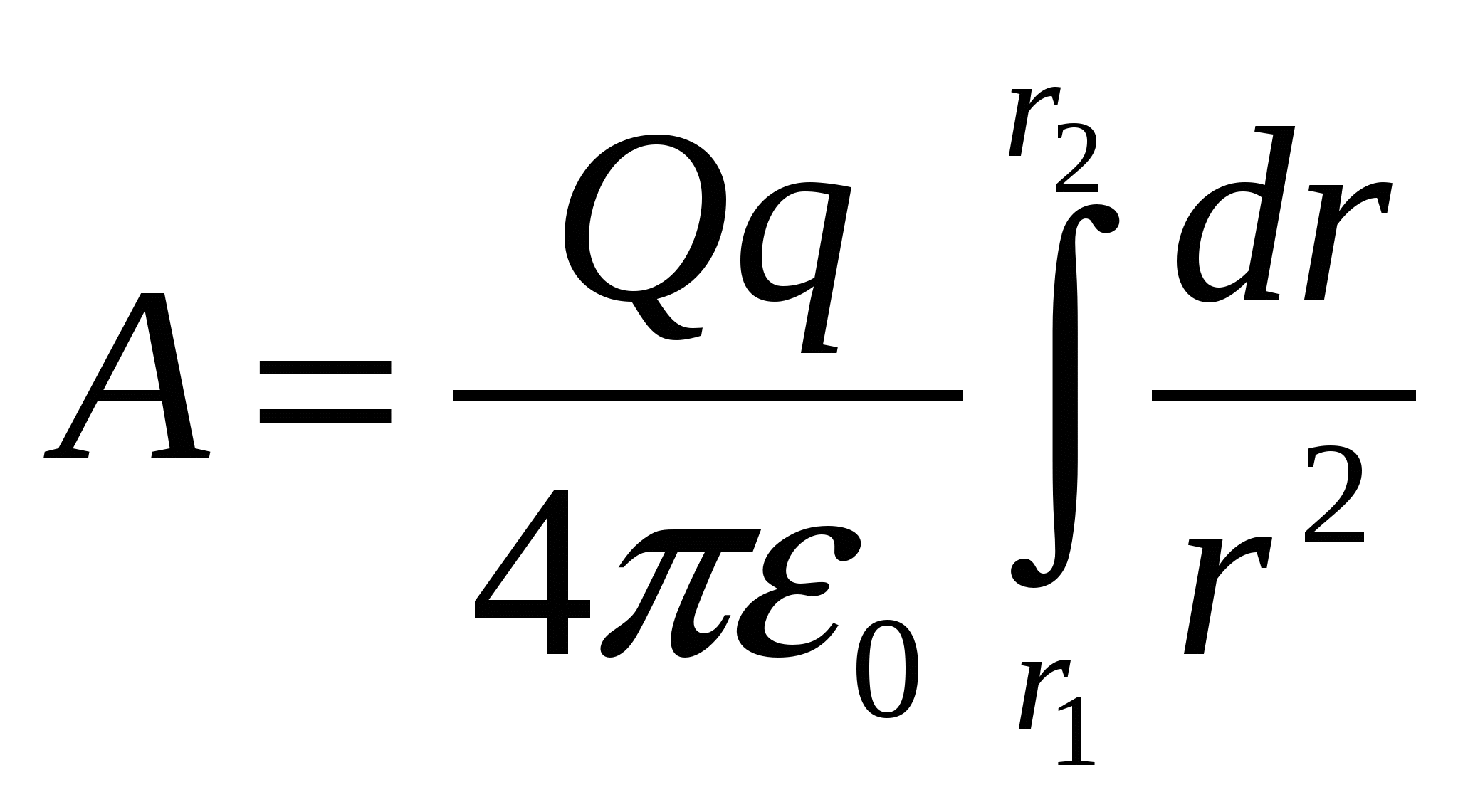 . Окончательно
. Окончательно
 , (1.18)
, (1.18)
Если заряд перемещается из точки A
в точку B
по другому пути, то, проделав такие же выкладки, снова придем к формуле (11.18). Следовательно, работа в электростатическом поле не зависит от формы пути, а зависит лишь от выбора начальной и конечной точки. Кроме того, как видно из (11.18), работа по перемещению заряда в электростатическом поде по замкнутому контуру равна нулю, т.е. 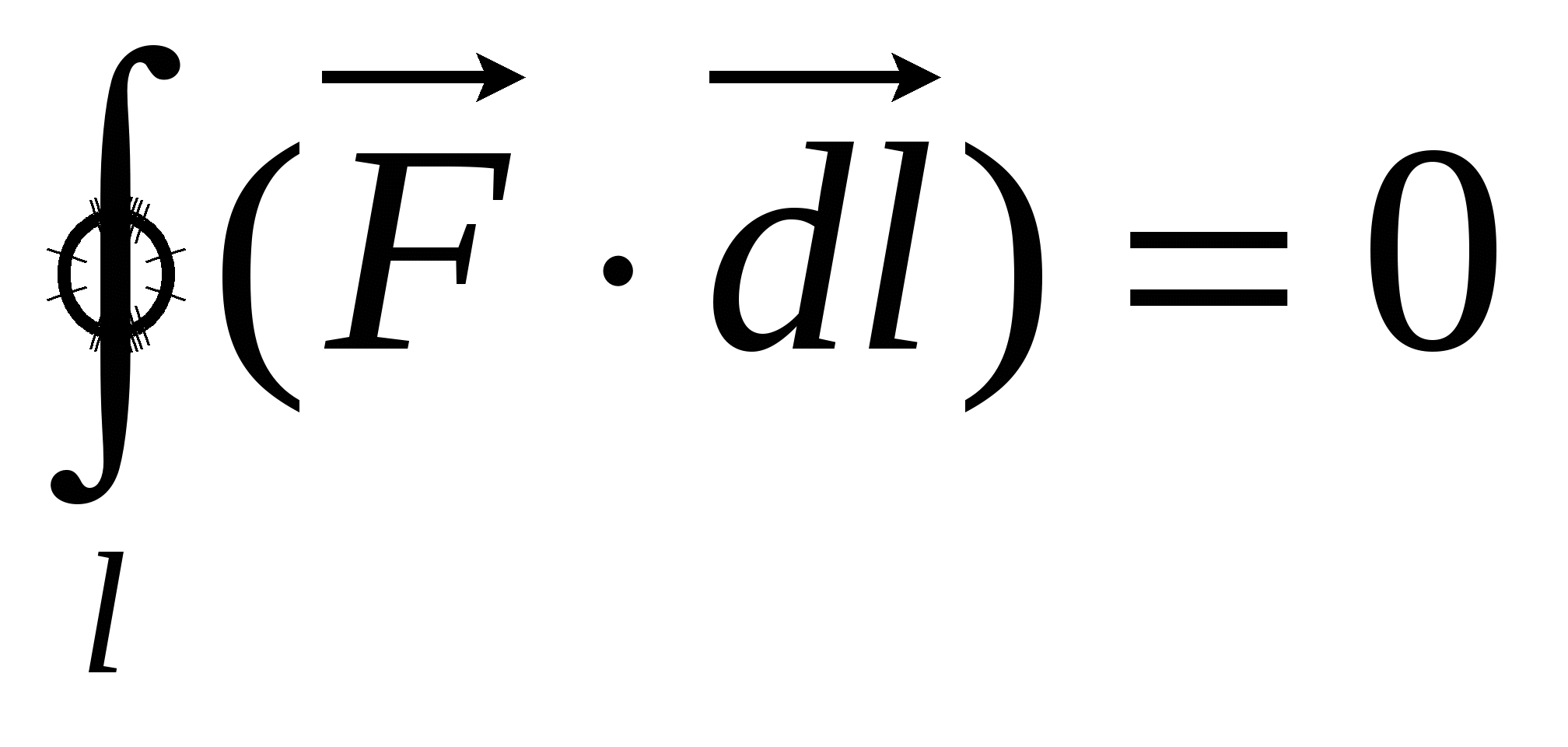 , (1.19)
, (1.19)
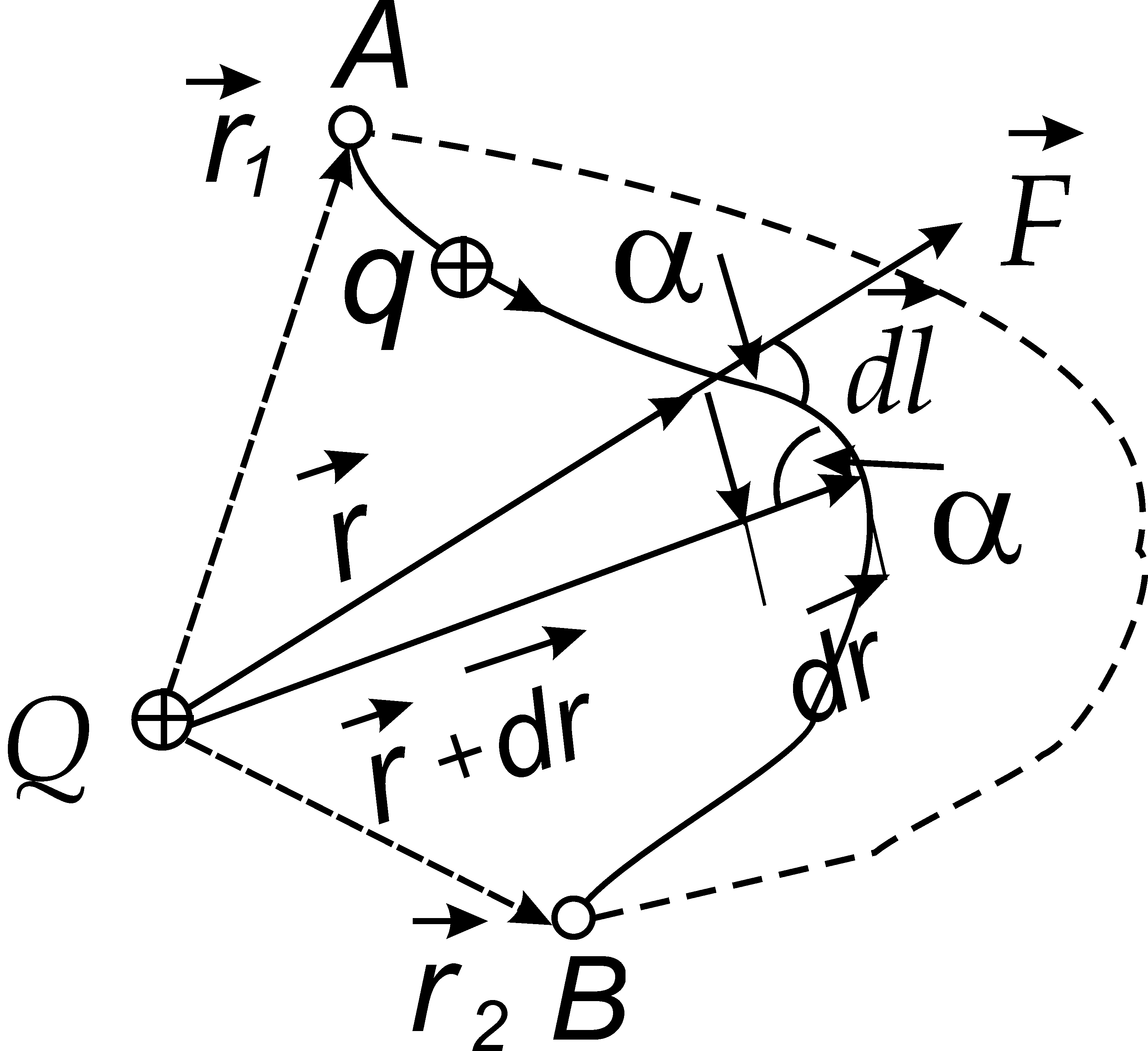
Рис. 1.11
Эти признаки означают, что электростатическое поле является потенциальным. В соответствии с результатом, полученным в § 3.3,работу потенциальных (консервативных) сил можно выразить через разность потенциальных энергий:
Из сопоставления (11.18) и (11.20) заключаем, что потенциальная энергия взаимодействия двух точечных зарядов
Единицей потенциала электростатического поляявляется вольт. Один вольт – это потенциал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией в 1 Дж: 1 В = 1 Дж/Кл.
Потенциал поля точечного заряда найдем, подставив (1.21) в (1.22):
 . . | (1.23) |
И, наконец, с помощью (1.22) выражение (1.20) для работы по перемещению заряда в электростатическом поле из одной точки в другую можно представить как произведение заряда на разность потенциалов:
равна нулю. Этот результат получен из того факта, что работа в электростатическом поле не зависит от формы пути. Поэтому равенство нулю циркуляции вектора есть также признак того, что электростатическое поле является потенциальным.
^
11.7. Связь между напряженностью поля и потенциалом
Поскольку электростатическое поле является потенциальным, то для него выполняется соотношение (3.17), устанавливающее связь между консервативной силой ж потенциальное энергией. Если в формулу (3.17) подставить
 ,
, то получим
то получим , (1.28)
, (1.28)т.е. напряженность электростатического поля равна градиенту потенциала, взятому со знаком "–"". Знак "–" указывает, что напряженность поля направлена в сторону убыли потенциала.
Введем понятие эквипотенциальной поверхности, т.е. поверхности, в любой точке которой значение потенциала одно и то же: φ =const . Для поля точечного заряда эквипотенциальные поверхности имеют сферическую форму, для равномерно заряженной нити – цилиндрическую и т. д.Вектор напряженности поля всегда перпендикулярен к эквипотенциальной поверхности.
Если потенциал является функцией только одной координаты x
, то выражение (1.28) упрощается:
Для однородного электростатического поля (например, поля плоского конденсатора) выражение (2.30) упрощается:
Проиллюстрируем применение формулы (11.32) на примерах.
1. Поле точечного заряда
3. Поле электрического диполя на перпендикуляре к его оси
5. Поле конденсатора
| . | (1.37) |
Бесконечная плоскость, заряженная с поверхностной плотностью заряда : для расчета напряженности электрического поля, созданного бесконечной плоскостью, выделим в пространстве цилиндр, ось которого перпендикулярна заряженной плоскости, а основания – параллельны ей и одно из оснований проходит через интересующую нас точку поля. Согласно теореме Гаусса поток вектора напряженности электрического поля сквозь замкнутую поверхность равен:
Ф= , с другой стороны он же: Ф=E
Приравняем правые части уравнений:
Выразим = - через поверхностную плотность заряда и найдем напряженность электрического поля:
Найдем напряженность электрического поля между разноименно заряженными пластинами с одинаковой поверхностной плотностью:
Найдем поле вне пластин:
Напряженность поля заряженной сферы
Ф= (2) т. Гаусса
для r < R
; , т.к. (внутри сферы нет зарядов)
Для r = R
( ; ; )
Для r > R
Напряженность поля, созданного шаром, заряженным равномерно по всему объему
Объемная плотность заряда,
распределенного по шару:
Для r < R
Для r = R
Для r > R
РАБОТА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА
Электростатическое поле
- эл. поле неподвижного заряда.
Fэл, действующая на заряд, перемещает его, совершая раборту.
В однородном электрическом поле Fэл = qE - постоянная величина
Работа поля (эл. силы)не зависит от формы траектории и на замкнутой траектории = нулю.
| В случае, если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль какой-либо траектории (рис. 1) двигается другой точечный заряд Q 0 , то сила, которая приложена к заряду, совершает некоторую работу. Работа силы F на элементарном перемещении dl равна Так как dl /cosα=dr, то Работа при перемещении заряда Q 0 из точки 1 в точку 2 (1) от траектории перемещения не зависит, а определяется только положениями начальной 1 и конечной 2 точек. Значит, электростатическое поле точечного заряда является потенциальным, а электростатические силы - консервативными Из формулы (1) видно, что работа, которая совершается при перемещении электрического заряда во внешнем электростатическом поле по произвольному замкнутому пути L, равна нулю, т.е. (2) Если в качестве заряда, которого перемещают в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути dl равна Еdl = E l dl , где E l = Ecosα - проекция вектора Е на направление элементарного перемещения. Тогда формулу (2) можно представить в виде (3) Интеграл называется циркуляцией вектора напряженности. Значит, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, которое обладает свойством (3), называетсяпотенциальным. Из равенства нулю циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они обязательно начинаются и кончаются на зарядах (на положительных или отрицательных) или же идут в бесконечность. Формула (3) верна только для электростатического поля. В дальнейшем будет показано, что с случае поля движущихся зарядов условие (3) не верно (для него циркуляция вектора напряженности отлична от нуля). |
Теорема о циркуляции для электростатического поля.
Поскольку электростатическое поле является центральным, то силы, действующие на заряд в таком поле, являются консервативными. Так как представляет собой элементарную работу, которую силы поля производят над единичным зарядом, то работа консервативных сил на замкнутом контуре равна
Потенциал
Система "заряд - электростатическое поле" или "заряд - заряд" обладает потенциальной энергией, подобно тому, как система "гравитационное поле - тело" обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называетсяпотенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал - это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
Потенциальная энергия поля - это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
Эту формулу можно представить в ином виде
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
Это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора.
Если имеется система двух заряженных проводников (конденсатор), то полная энергия системы равна сумме собственных потенциальных энергий проводников и энергии их взаимодействия:
Энергия электростатического поля системы точечных зарядов равна:
Равномерно заряженная плоскость.
Напряжённость электрического поля, создаваемого бесконечной плоскостью, заряженной с поверхностной плотностью заряда , можно рассчитать, воспользовавшись теоремой Гаусса.
Из условий симметрии следует, что вектор E
везде перпендикулярен плоскости. Кроме того, в симметричных относительно плоскости точках вектор E
будет одинаков по величине и противоположен по направлению.
В качестве замкнутой поверхности выберем цилиндр, ось которого перпендикулярна плоскости, а основания расположены симметрично относительно плоскости, как показано на рисунке.
Так как линии напряжённости параллельны образующим боковой поверхности цилиндра, то поток через боковую поверхность равен нулю. Поэтому поток вектораЕ
через поверхность цилиндра
где - площадь основания цилиндра. Цилиндр вырезает из плоскости заряд . Если плоскость находится в однородной изотропной среде с относительной диэлектрической проницаемостью , то
Когда напряженность поля не зависит от расстояния между плоскостями, такое поле называют однородным. График зависимости E (x ) для плоскости.
Разность потенциалов между двумя точками, находящимися на расстояниях R 1 и R 2 от заряженной плоскости, равна
Пример 2. Две равномерно заряженные плоскости.
Рассчитаем напряжённость электрического поля, создаваемого двумя бесконечными плоскостями. Электрический заряд распределен равномерно с поверхностной плотностями и . Напряженность поля найдем как суперпозицию напряжённостей полей каждой из плоскостей. Электрическое поле отлично от нуля только в пространстве между плоскостями и равно .
Разность потенциалов между плоскостями , где d -
расстояние между плоскостями.
Полученные результаты могут быть использованы для приближённого расчета полей, создаваемых плоскими пластинами конечных размеров, если расстояния между ними много меньше их линейных размеров. Заметные погрешности таких расчётов появляются при рассмотрении полей вблизи краев пластин. График зависимости E
(x
) для двух плоскостей.
Пример 3. Тонкий заряженный стержень.
Для расчёта напряжённости электрического поля, создаваемого очень длинным заряженным с линейной плотностью заряда стержнем, используем теорему Гаусса.
На достаточно больших расстояниях от концов стержня линии напряжённости электрического поля направлены радиально от оси стержня и лежат в плоскостях, перпендикулярных этой оси. Во всех точках, равноудалённых от оси стержня, численные значения напряжённости одинаковы, если стержень находится в однородной изотропной среде с относительной диэлектрической
проницаемостью .
Для расчета напряженности поля в произвольной точке, находящейся на расстоянииr
от оси стержня, проведём через эту точку цилиндрическую поверхность
(см. рисунок). Радиус этого цилиндра равен r
, а его высота h
.
Потоки вектора напряжённости через верхнее и нижнее основания цилиндра будут равны нулю, так как силовые линии не имеют составляющих, нормальных к поверхностям этих оснований. Во всех точках боковой поверхности цилиндра
Е
= const.
Следовательно, полный поток вектора E
через поверхность цилиндра будет равен
По теореме Гаусса, поток вектора E равен алгебраической сумме электрических зарядов, находящихся внутри поверхности (в данном случае цилиндра) делённой на произведение электрической постоянной и относительной диэлектрической проницаемости среды
где заряд той части стержня, которая находится внутри цилиндра. Следовательно, напряжённость электрического поля
Разность потенциалов электрического поля между двумя точками, находящимися на расстояниях R 1 и R 2 от оси стержня, найдём, пользуясь связью между напряжённостью и потенциалом электрического поля. Так как напряжённость поля изменяется только в радиальном направлении, то
Пример 4. Заряженная сферическая поверхность.
Электрическое поле, создаваемое сферической поверхностью, по которой равномерно распределён электрический заряд с поверхностной плотностью , имеет центрально-симметричный характер.
Линии напряжённости направлены по радиусам от центра сферы, а модуль вектораE
зависит только от расстояния r
от центра сферы. Для расчёта поля выберем замкнутую сферическую поверхность радиуса r
.
При r o
Напряжённость поля равна нулю, так как внутри сферы заряд отсутствует.
При r > R (вне сферы), согласно теореме Гаусса
где - относительная диэлектрическая проницаемость среды, окружающей сферу.
Напряжённость уменьшается по тому же закону, что и напряженность поля точечного заряда, т. е. по закону .
При r o
График зависимости E
(r
) для сферы.
Пример 5. Заряженный по объему шар из диэлектрика.
Если шар радиусом R
из однородного изотропного диэлектрика с относительной проницаемостью равномерно заряжен по объёму с плотностью , то создаваемое им электрическое поле также является центрально-симметричным.
Как и в предыдущем случае, выберем замкнутую поверхность для расчёта потока вектора E
в виде концентрической сферы, радиус которой r
может изменяться от 0 до .
При r
< R
поток вектора E
через эту поверхность будет определяться зарядом
Так что
При r
< R
(внутри шара) .
Внутри шара напряжённость возрастает прямо пропорционально расстоянию от центра шара. Вне шара (при r
> R
) в среде с диэлектрической проницаемостью , поток вектора E
через поверхность будет определяться зарядом .
При r o >R o (вне шара) .
На границе "шар - окружающая среда" напряжённость электрического поля изменяется скачком, величина которого зависит от соотношения диэлектрических проницаемостей шара и среды. График зависимости E
(r
) для шара ().
Вне шара (r > R ) потенциал электрического поля меняется по закону
.
Внутри шара (r < R ) потенциал описывается выражением
В заключение, приведем выражения для расчета напряженностей полей заряженных тел, различной формы
| Разность потенциалов | |
| Напряжение - разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! | |
| Единица разности потенциалов Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
Проводник – это твердое тело, в котором имеются “свободные электроны”, перемещающиеся в пределах тела.
Металлические проводники в целом являются нейтральными: в них поровну отрицательных и положительных зарядов. Положительно заряженные – это ионы в узлах кристаллической решетки, отрицательные – электроны, свободно перемещающиеся по проводнику. Когда проводнику сообщают избыточное количество электронов, он заряжается отрицательно, если же у проводника «отбирают» какое-то количество электронов, он заряжается положительно.
Избыточный заряд распределяется только по внешней поверхности проводника.
1 . Напряженность поля в любой точке внутри проводника равна нулю.
2 . Вектор на поверхности проводника направлен по нормали к каждой точке поверхности проводника.
Из того факта, что поверхность проводника эквипотенциальна следует, что непосредственно у этой поверхности поле направлено по нормали к ней в каждой точке (условие 2 ). Если бы это было не так, то под действием касательной составляющей заряды пришли бы в движение по поверхности проводника. т.е. равновесие зарядов на проводнике было бы невозможным.
Из 1 следует, что поскольку
Внутри проводника избыточных зарядов нет .
Заряды распределяются только на поверхности проводника с некоторой плотностью s и находятся в очень тонком поверхностном слое (его толщина около одного-двух межатомных расстояний).
Плотность заряда - это количество заряда, приходящееся на единицу длины, площади или объёма, таким образом определяются линейная, поверхностная и объемная плотности заряда, которые измеряются в системе СИ: в Кулонах на метр [Кл/м], в Кулонах на квадратный метр [Кл/м²] и в Кулонах на кубический метр [Кл/м³], соответственно. В отличие от плотности вещества, плотность заряда может иметь как положительные, так и отрицательные значения, это связано с тем, что существуют положительные и отрицательные заряды.
Общая задача электростатики
Вектор напряженности ,
по теореме Гаусса
Уравнение Пуассона.
В случае - нет зарядов между проводниками, получаем
- уравнение Лапласа.
Пусть известны граничные условия на поверхностях проводников: значения ; тогда данная задача имеет единственное решение согласно теореме единственности.
При решении задачи определяется значение и затем поле между проводниками определяется распределение зарядов на проводниках (по вектору напряженности у поверхности).
Рассмотрим пример. Найдем напряженность в пустой полости проводника.
Потенциал в полости удовлетворяет уравнению Лапласа;
потенциал на стенках проводника .
Решение уравнения Лапласа в этом случае тривиальное, и по теореме единственности других решений нет
, т.е. поля в полости проводника нет.
Уравне́ние Пуассо́на - эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает
· электростатическое поле,
· стационарное поле температуры,
· поле давления,
· поле потенциала скорости в гидродинамике.
Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.
Это уравнение имеет вид:
где - оператор Лапласа или лапласиан, а - вещественная или комплексная функция на некотором многообразии.
В трёхмерной декартовой системе координат уравнение принимает форму:
В декартовой системе координат оператор Лапласа записывается в форме и уравнение Пуассона принимает вид:
Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа - частный случай уравнения Пуассона):
Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм - «релаксационный метод».
| Будем рассматривать уединенный проводник, т. е. проводник, значительно удаленный от других проводников, тел и зарядов. Его потенциал, как известно, прямо пропорционален заряду проводника. Из опыта известно, что разные проводники, будучи при этом одинаково заряженными, имеют различные потенциалы. Поэтому для уединенного проводника можно записать Величину (1) называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника задается зарядом, сообщение которого проводнику изменяет его потенциал на единицу. Емкость уединенного проводника зависит от его размеров и формы, но не зависит от материала, формы и размеров полостей внутри проводника, а также его агрегатного состояния. Причиной этому есть то, что избыточные заряды распределяются на внешней поверхности проводника. Емкость также не зависит ни от заряда проводника, ни от его потенциала. Единица электроемкости - фарад (Ф): 1 Ф - емкость такого уединенного проводника, у которого потенциал изменяется на 1 В при сообщении ему заряда 1 Кл. Согласно формуле потенциала точечного заряда, потенциал уединенного шара радиуса R, который находится в однородной среде с диэлектрической проницаемостью ε, равен Применяя формулу (1), получим, что емкость шара (2) Из этого следует, что емкостью 1 Ф обладал бы уединенный шар, находящийся в вакууме и имеющий радиус R=C/(4πε 0)≈9 10 6 км, что примерно в 1400 раз больше радиуса Земли (электроемкость Земли С≈0,7 мФ). Следовательно, фарад - довольно большая величина, поэтому на практике применяются дольные единицы - миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ). Из формулы (2) следует также, что единица электрической постоянной ε 0 - фарад на метр (Ф/м) (см. (78.3)). |
Конденса́тор (от лат. condensare - «уплотнять», «сгущать») - двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накоплениязаряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками ), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
Мкость
Основной характеристикой конденсатора является его ёмкость , характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (q = CU ). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до тысяч микрофарад. Однако существуют конденсаторы (ионисторы) с ёмкостью до десятков фарад.
Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга, в системе СИ выражается формулой: , где -относительная диэлектрическая проницаемость среды, заполняющей пространство между пластинами (в вакууме равна единице), - электрическая постоянная, численно равная 8,854187817·10 −12 Ф/м. Эта формула справедлива, лишь когда d много меньше линейных размеров пластин.
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.
При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счёт разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна
Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.
Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.
[править]Удельная ёмкость
Конденсаторы также характеризуются удельной ёмкостью - отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.
В электрических цепях применяются различные способы соединения конденсаторов . Соединение конденсаторов может производиться: последовательно , параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Рисунок 1. Способы соединения конденсаторов.
>>Физика: Напряженность электрического поля. Принцип суперпозиции полей
Недостаточно утверждать, что электрическое поле существует. Надо ввести количественную характеристику поля. После этого электрические поля можно будет сравнивать друг с другом и продолжать изучать их свойства.
Электрическое поле обнаруживается по силам, действующим на заряд. Можно утверждать, что мы знаем о поле все, что нам нужно, если будем знать силу, действующую на любой заряд в любой точке поля.
Поэтому надо ввести такую характеристику поля, знание которой позволит определить эту силу.
Если поочередно помещать в одну и ту же точку поля небольшие заряженные тела и измерять силы, то обнаружится, что сила, действующая на заряд со стороны поля, прямо пропорциональна этому заряду. Действительно, пусть поле создается точечным зарядомq 1
. Согласно закону Кулона (14.2) на заряд q 2
действует сила, пропорциональная заряду q 2
. Поэтому отношение силы, действующей на помещаемый в данную точку поля заряд, к этому заряду для каждой точки поля не зависит от заряда и может рассматриваться как характеристика поля. Эту характеристику называютнапряженностью электрического поля. Подобно силе, напряженность поля – векторная величина
; ее обозначают буквой . Если помещенный в поле заряд обозначить через q
вместо q 2
, то напряженность будет равна:

Отсюда сила, действующая на заряд q со стороны электрического поля, равна:

Напряженность поля точечного заряда. Найдем напряженность электрического поля, создаваемого точечным зарядом q 0 . По закону Кулона этот заряд будет действовать на положительный заряд q с силой, равной

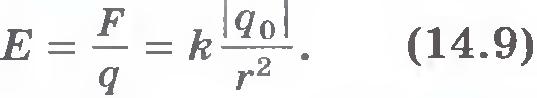


если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых
 и т. д., то результирующая напряженность поля в этой точке равна сумме напряженностей этих полей:
и т. д., то результирующая напряженность поля в этой точке равна сумме напряженностей этих полей:
причем напряженность поля, создаваемая отдельным зарядом, определяется так, как будто других зарядов, создающих поле, не существует.
Благодаря принципу суперпозиции для нахождения напряженности поля системы заряженных частиц в любой точке достаточно знать выражение (14.9) для напряженности поля точечного заряда. На рисунке 14.8 показано, как определяется напряженность поля в точке A
, созданная двумя точечными зарядами q 1
и q 2 , q 1 >q 2
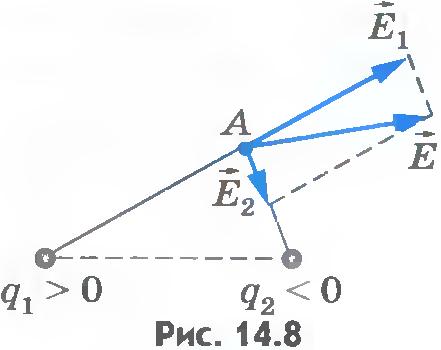
???
1. Что называется напряженностью электрического поля?
2. Чему равна напряженность поля точечного заряда?
3. Как направлена напряженность поля зарядаq 0 , если q 0
>0
? если q 0
<0
?
4. Как формулируется принцип суперпозиции полей?
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский, Физика 10 класс
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиЕсли у вас есть исправления или предложения к данному уроку,



